Project Setup

Within this section a simple test project is defined, which will be refined in the subsequent sections to show how to do parameter scans, and to demonstrate how to define more complicated geometries.

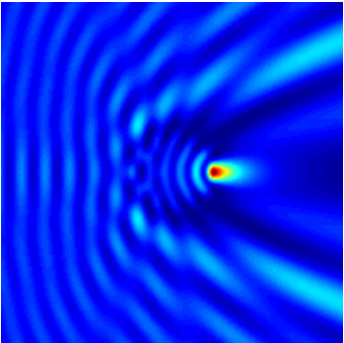
We regard the light scattering off an infinite glass rod. The project is called mie2D. Figure “Test example” shows the setup.

_images/example_geometry.png

Test example

An incoming plane wave is scattered off an infinite rod.

In this section we use fixed project parameters: The surroundings consists of air. The incoming light field has a vacuum wavelength of 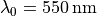\lambda_0 = 550\,\runits{nm} and is polarized in z-direction with amplitude equal to one. Hence, the illuminating field is given as

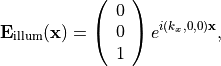
\begin{eqnarray*} \VField{E}_{\mathrm{illum}}(\pvec{x}) = \left ( \begin{array}{c} 0 \\ 0 \\ 1 \end{array} \right ) e^{i (k_x, 0, 0) \pvec{x}}, \end{eqnarray*}

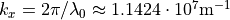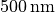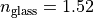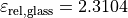with k_x = 2\pi/\lambda_0 \approx 1.1424 \cdot 10^7\mathrm{m}^{-1}. The glass rod has a cross-section diameter of 500\,\runits{nm} and a refractive index of n_{\mathrm{glass}}=1.52, which gives a relative permittivity of \varepsilon_{\mathrm{rel, glass}}=2.3104.

The input files to this project are given below. The project file mie2D.jcmp defines two post-processes. The first post-process computes the electromagnetic energy flux of the scattered field into the exterior domain. Up to normalization this is the integral scattering cross-section. The second post-process exports the computed field onto a Cartesian mesh.

The following driver run.m shows how to run the project in Matlab:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
%% run the project
results = jcmwave_solve('mie2D.jcmp');

%% get scattering cross section
scattering_cross_section = ...
  results{2}.ElectromagneticFieldEnergyFlux{1};
fprintf('\nscattering cross section: %.8g\n', ...
        real(scattering_cross_section)); 


%% plot exported cartesian grid within matlab:
cfb = results{3};
amplitude = cfb.field{1};
intensity = sum(conj(amplitude).*amplitude, 3);
pcolor(cfb.X, cfb.Y, intensity); 
shading interp; view(0, 90); axis equal;

In line 2, the project is solved. The computed data is returned as a cell array, where results{1} refers to the fieldbag and the subsequent entries refer to result data of the post-processes. This way we can extract the scattering cross-section in lines 5 and 6. With lines 12-16 we plot the computed intensity, which was exported on a regular Cartesian grid, see Figure “Intensity”.

_images/intensity.png

Intensity

Pseudo-color intensity plot as produced by the driver run.m.

For visualization of the computed fields you may also use the JCMview-tool which is available within Matlab by the wrapper jcmwave_view.m:

jcmwave_view(results{1}.file);

Here, results{1}.file is the file path to the computed solution fieldbag.

In the above driver run.m we have used the command jcmwave_solve, which automatically created the finite element mesh, solved the problem and loaded the result data. Often, when setting up a new project, you may first want to check if the geometry has been defined properly. To do this, call the mesh generator separately (driver run_geo.m):

%% generate mesh file only
jcmwave_geo('.');

%% open grid.jcm in JCMview
jcmwave_view('grid.jcm');

The next section Keyword Substitution shows how we can parameterize our test problem.

.jcm Input Files

  • layout.jcm [ASCII]

     1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
    Layout {
  UnitOfLength = 1e-6

  MeshOptions {
    MaximumSidelength = 0.1
  }

  # Computational domain
  Parallelogram {
    DomainId = 1
    Width = 4
    Height = 4

    # set transparent boundary conditions
    BoundarySegment {
      BoundaryClass = Transparent
    }
  }

  # Scatterer (rod)
  Circle {
    DomainId = 2
    Radius = 0.5
    RefineAll = 4
  } 
}

  • materials.jcm [ASCII]

     1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
    
# material properties for the surroundings (air)
Material {
  DomainId = 1
  RelPermittivity = 1.0
  RelPermeability = 1.0
}

# material properties the glass rod
Material {
  DomainId = 2
  RelPermittivity = 2.3104 # 1.52^2
  RelPermeability = 1.0
}

  • sources.jcm [ASCII]

     1
 2
 3
 4
 5
 6
 7
 8
 9
10
    SourceBag {
  Source {
    ElectricFieldStrength {
      PlaneWave {
        K = [1.14239732857811e7 0.0 0.0]
        Amplitude = [0 0 1]
      }
    }
  }
}

  • mie2D.jcmp [ASCII]

     1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
    Project {
  InfoLevel = 3
  Electromagnetics {
    TimeHarmonic {
      Scattering {
        FieldComponents = Electric
        Accuracy {
					FiniteElementDegree = 3	
          Refinement {
            MaxNumberSteps = 0
            PreRefinements = 0
          }
        }
      }
    }
  }
}

# computes the energy flux of the scattered field into the exterior domain
PostProcess {
  FluxIntegration {
    FieldBagPath = "./mie2D_results/fieldbag.jcm"
    OutputFileName = "./mie2D_results/energyflux_scattered.jcm"  
    OutputQuantity = ElectromagneticFieldEnergyFlux
    InterfaceType = ExteriorDomain
  }
}

# exports computed field on cartesian grid 
PostProcess {
  ExportFields {
    FieldBagPath = "./mie2D_results/fieldbag.jcm"
    OutputFileName = "./mie2D_results/fieldbag_cartesian.jcm"
    Cartesian {
      NGridPointsX=200
      NGridPointsY=200
    }
  }
}