Matlab Code SnippetsΒΆ

So far, only a simple keyword substitution was used within the .jcmt input files. This section demonstrates how to embed Matlab code blocks. Before we do this, we update our Matlab driver:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
%% set problem parameter
keys.radius = 0.3; 
keys.n_air = 1.0;
keys.n_glass = 1.52;
keys.lambda_0 = 0.550; % in um 
keys.polarization = 45; % in degree
  
%% run the project
results = jcmwave_solve('mie2D.jcmp', keys);

%% get scattering cross section
scattering_cross_section = ...
  results{2}.ElectromagneticFieldEnergyFlux{1};
fprintf('\nscattering cross section: %.8g\n', ...
        real(scattering_cross_section)); 

%% plot exported cartesian grid within matlab:
cfb = results{3};
amplitude = cfb.field{1};
intensity = sum(conj(amplitude).*amplitude, 3);
pcolor(cfb.X, cfb.Y, intensity); 
shading interp; view(0, 90); axis equal;

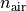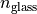Now, more parameters are in use: The refractive indices of the two materials, n_\mathrm{air} and n_\mathrm{glass}, the vacuum wavelength 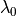\lambda_0 of the illumination plane wave (in 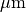\runits{\mu m}), and the polarization of the incoming field, that is

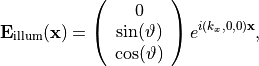
\begin{eqnarray*} \VField{E}_{\mathrm{illum}}(\pvec{x}) = \left ( \begin{array}{c} 0 \\ \sin(\vartheta) \\ \cos(\vartheta) \end{array} \right ) e^{i (k_x, 0, 0) \pvec{x}}, \end{eqnarray*}

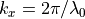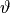with k_x = 2\pi/\lambda_0, and \vartheta the angle given by the value of the key polarization.

To process the new input parameters, the files materials.jcm and sources.jcm have been replaced with materials.jcmt and sources.jcmt, which now contain embedded Matlab blocks. A Matlab block starts with the tag <? and is closed by ?>. For example, materials.jcmt begins with the following Matlab block:

1
2
3
4
5
<? 
  % compute rel. permittivity of glass from 
  % refractive index
  keys.permittivity_air = keys.n_air^2; 
?>

Within a Matlab block, any Matlab command can be used, and one has access to the parameter container keys as passed to jcmwave_solve.m. As can be seen in line 4, it is allowed to update the parameter container. There, we compute the relative permittivity from the given refractive index. Later this newly created parameter is used (line 10):

  RelPermittivity = %(permittivity_air)e

The same is repeated for the material section of the glass rod (line 14-18 in materials.jcmt).

The updated source file sources.jcmt shows a less trivial Matlab code block:

1
2
3
4
5
6
7
<?
  % compute k-vector and e-vector
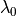  lambda_0 = keys.lambda_0*1e-6; % initially in um! 
  keys.k_illum = [2*pi/lambda_0*keys.n_air 0 0];
  pol_degree = keys.polarization;
  keys.e_illum = [0 sind(pol_degree) cosd(pol_degree)]; 
?>

Here, we compute the wave vector \pvec{k}_{\mathrm{illum}} and amplitude vector \VField{E_{\mathrm{illum}}} of the incoming plane wave from the vacuum wavelength \lambda_0, the refractive index of air (trivial) and the polarization angle 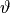\vartheta. Later, within a .jcm block, these vectors are used to define the illuminating plane wave:

      PlaneWave {
        K = %(k_illum)e
        Amplitude = %(e_illum)e
      }

The next section Loops shows how to use embedded scripting to define more complicated geometries.

Updated Input Files

  • materials.jcmt [ASCII]

     1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
    <? 
  % compute rel. permittivity of glass from 
  % refractive index
  keys.permittivity_air = keys.n_air^2; 
?>

# material properties for the surroundings (air)
Material {
  DomainId = 1
  RelPermittivity = %(permittivity_air)e
  RelPermeability = 1.0
}

<? 
  % compute rel. permittivity of glass from 
  %  refractive index
  keys.permittivity_glass = keys.n_glass^2; 
?>

# material properties the glass rod
Material {
  DomainId = 2
  RelPermittivity = %(permittivity_glass)e
  RelPermeability = 1.0
}

  • sources.jcmt [ASCII]

     1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
    <?
  % compute k-vector and e-vector
  lambda_0 = keys.lambda_0*1e-6; % initially in um! 
  keys.k_illum = [2*pi/lambda_0*keys.n_air 0 0];
  pol_degree = keys.polarization;
  keys.e_illum = [0 sind(pol_degree) cosd(pol_degree)]; 
?>


SourceBag {
  Source {
    ElectricFieldStrength {
      PlaneWave {
        K = %(k_illum)e
        Amplitude = %(e_illum)e
      }
    }
  }
}