PeriodicLineSource¶
| Type: | section |
|---|---|
| Appearance: | multiple |
Defines time-harmonic, Bloch-periodic, singular electric current densities on  -coordinate directed lines arranged in a onefold periodic arrangement int the
-coordinate directed lines arranged in a onefold periodic arrangement int the  -plane.
-plane.
![\begin{eqnarray*}
\VField{J}(\pvec{x}, t) & = & \sum_{l=-\infty}^{l=\infty} e^{i\cdot l \cdot (k_x\cdot a_x + k_y\cdot a_y)} \VField{j} \delta \left( [x, y]-[x_0, y_0]-l \cdot [a_x, a_y] \right) e^{ik_z (z-z_0)}e^{-i \omega t}
\end{eqnarray*}](_images/math/57661cdb26db4832f80d9aba7e10f47bba502134.png)
Here, ![\pvec{a} = [a_x, a_y]](_images/math/64a688d4b2549917ccaaa6036644e002da7a1bca.png) is the lattice vector,:math:omega is the the angular frequency,
is the lattice vector,:math:omega is the the angular frequency,  is the wave vector in
is the wave vector in  -direction,
-direction, ![\pvec{x}_0 = [x_0; y_0; z_0]](_images/math/808abd77a3422ce08f01afba9db592f1d26c3e92.png) is the position of the line source in the unit cell and
is the position of the line source in the unit cell and 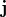 is a constant strength vector. The lattice vector is determined from the specified geometry. Other parameters are set using Omega, K, Position, and Strength, respectively.
is a constant strength vector. The lattice vector is determined from the specified geometry. Other parameters are set using Omega, K, Position, and Strength, respectively.