Positions¶
| Type: | section |
|---|---|
| Appearance: | multiple |
This section defines positions in the lattice where the structure is replicated. For example, with the definition
Positions {
DomainId=2
Range1=[-1 3]
Range2=[0 1]
}
the structure is replicated at positions displaced by 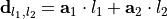 with
with 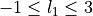 and
and 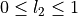 , setting
, setting DomainId=2. It is possible to use multiple Position sections with different domain identifiers.
Alternatively, one can provide a matrix DomainIds whose form visually resembles the structure to be created:
Positions {
RangeStart = [0 0]
DomainIds = [0 0 0 0 2 0 2 0 0 0 0;
0 0 0 2 2 0 2 2 0 0 0;
0 0 2 2 2 0 2 2 2 0 0;
0 2 2 2 2 0 2 2 2 2 0;
2 2 2 2 2 0 2 2 2 2 2]
}
Here 0 stands for an omitted structure. The DomainId entries 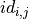 in the
in the DomainIds (row index  , column indices,
, column indices,  ), are related to the cell offset indices
), are related to the cell offset indices 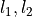 by
by
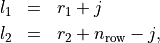
where 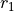 and
and  are the entries of the
are the entries of the RangeStart vector. Hence, the lower left entry in the matrix refers to the RangeStart index.
For an hexagonal lattice, i.e. LatticeAngle=60, the definition
Positions {
Range1 = [0 5]
Range2 = [0 5]
}
results in the following structure:
With the parameter IndexVectorY the lattice position  is shifted each second row by the value
is shifted each second row by the value 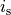 , that is
, that is
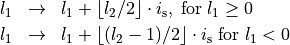
Setting ``IndexVectorY``= -1 yields:

