LinearThermalExpansibility¶
| Type: | 2-Tensor, or section |
|---|---|
| Range: | [v_1, …, v_9] |
| Default: | -/- |
| Appearance: | optional |
Sets the linear thermal expansion coefficient 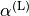 is the fractional change of length of an infinitesimal small body per degree of temperature change, that is
is the fractional change of length of an infinitesimal small body per degree of temperature change, that is

Units are  . Since the length changes may be anisotropic the thermal expansion coefficient is a rank-2 tensor.
. Since the length changes may be anisotropic the thermal expansion coefficient is a rank-2 tensor.
A constant linear thermal expansion coefficient can be defined by assigning a rank-2 tensor:
Material {
# defines a constant conductivity
LinearThermalExpansibility =
[..., ..., ...
..., ..., ...
..., ..., ...]
}
Assign a scalar for an isotropic thermal expansibility.
For more general cases, the thermal expansibility may be given as a section in order to deal with space, time, and parameter dependent definitions:
# define the density as a section
LinearThermalExpansibility {
Python {...}
...
}
Field definitions within the section LinearThermalExpansibility are summed up. Consult the subsequent sections to see which types of field definitions are allowed.