ThermoOpticalCorrection¶
| Type: | section |
|---|---|
| Appearance: | multiple |
The thermo-optical correction describes the temperature (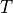 ) dependency of the relative permittivity in a linear sense near a specified temperature
) dependency of the relative permittivity in a linear sense near a specified temperature 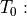
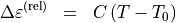
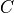 is the thermo-optical coefficient. It is a
is the thermo-optical coefficient. It is a 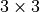 - matrix to cover anisotropic effects. The total relative permittivity is then given by
- matrix to cover anisotropic effects. The total relative permittivity is then given by
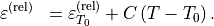
For too large temperature differences the linear correction term may loose its validity. To prevent obscure relative permittivity definitions one may restrict the absolute value of the correction term by a threshold value  ,
,
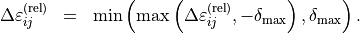
The JCM - syntax looks like this:
# define the relative permittivity with thermo-optical correction
RelPermittivity {
# define temperature independent terms
Constant = ...
...
ThermoOpticalCorrection {
T0 = ... # set correction free temperature
C = ... # set thermo-optical coefficients
CutOff .. # set threshold here
}
}
Warning
Often, the thermo-optical coefficient is defined as a refractive index - temperature relation, 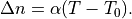
In a linear sense both definitions are equivalent:
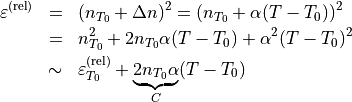
The approximation in the last line is due to linearization.