Accuracy¶

Type:	section
Appearance:	simple

The settings of this section control the numerical accuracy of the simulation setup.

Note

To ease the usage JCMsolve aims to automatically adapt numerical settings. As an ultimate goal we only want you to specify a single Precision value which should be reached with smallest numerical costs. However, with some physical insight and a basic understanding of Finite Element convergence, the user can accelerate computations by tuning the numerical parameters.

Guideline for the user

If the user has special knowledge about the physics of the expected solution, a user-adapted mesh can enhance convergence and increase accuracy and speed of simulations. For electromagnetic projects following rules are good practice:

For wave propagation problems apply local mesh options in JCMgeo such that patch sizes are about the wavelength in the given material.
At metal or high index contrast corners, where the solution is expected to have singularities, refine the mesh locally in advance within JCMgeo.
Use Precision (or PrecisionFarField for scattering problems) to define your goal precision.
If the field is expected to have strong singularities or to check the convergence, use the adaptive refinement loop (see Refinement). Check how many mesh refinements are needed to reach the desired accuracy of your output quantity.

Accuracy parameters of the Finite Element Method

The Finite Element Method represents the solution field of a partial differential equation in a discrete subspace of an infinite dimensional function space, in which the true physical solution resides. This Finite Element subspace is created in two steps. First, the underlying geometrical layout is subdivided into a finite number of sub patches. Then, on each of the patches a number of local polynomial ansatz functions is defined. The Finite Element solution is a superposition of all local ansatz functions on all patches.

In order to increase accuracy of the Finite Element solution, the discrete ansatz space has to be enlarged. In general, this can be achieved by making the mesh finer, i.e., decreasing size 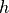$h$ of the patches, or by increasing the polynomial degree $p$ on the patches. For the error of the solution following estimation is often valid:

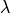$\begin{eqnarray*} \mathrm{error} & \propto & \left( \frac{h}{\lambda} \right)^p, \end{eqnarray*}$

where $\lambda$ is a typical length scale (e.g. the local wavelength).

Hence, increasing polynomial order $p$ seems favorable, because it leads to exponential decrease of the error. If however the solution is only $k<p$ times continuously differentiable, the error is bound by $h^k$ and increasing $p$ does no longer increase accuracy with an exponential rate. 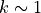This precisely happens at corners of the geometry where singularities of the solution may arise leading to a severe lack of regularity with $k \sim 1$ . There the local convergence of the finite element approximation is better described by

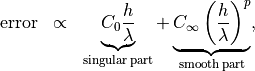
$\begin{eqnarray*} \mathrm{error} & \propto & \underbrace{C_0 \frac{h}{\lambda} }_{\mathrm{singular\,part}} + \underbrace{C_\infty \left( \frac{h}{\lambda} \right)^p}_{\mathrm{smooth\,part}}, \end{eqnarray*}$

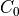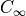with local constants $C_0$ and $C_\infty$ . Now, the situation looks different. You only benefit from higher-order finite elements as long as the smooth part dominates the local error. Otherwise a mesh refinement is more efficient. This can be either performed by the user within the meshing tool JCMgeo (e.g. refinements at corners) or by automatic mesh refinements within JCMsolve.

Note

The above error representation refers to the near field approximation of the solution. For scattering computations the far field approximation is typically requested. Often the far field error is much more insensitive to the singular part than for the near field error. Practically, this implies that fewer (or no) mesh refinements are needed to reach the desired accuracy in the far field data.

Controlling mesh size 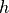$h$ and polynomial degree $p$

The better 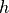$h$ and $p$ are adapted to the true physical solution, the more efficient the Finite Element simulation becomes. Because the true solution is unknown in advance, JCMsolve provides sophisticated a priori estimation techniques to set up the Finite Element parameters with minimal user input.

The mesh generation tool JCMgeo subdivides the user defined geometry into small patches and allows the definition of maximum mesh sizes for different parts of the geometrical setup. The mesh is read by JCMsolve and Finite Element degrees are set on the cells of the mesh afterwards. The Precision controls the self-adaptive setup of the Finite Element degrees on the mesh and only requires the user to define a single accuracy level. The polynomial degree $p$ is adapted automatically on each individual patch of the mesh in order to obtain well-balanced accuracy of the solution with maximum efficiency.

Refinement loop

In addition to above a priori Precision settings, applied before the simulation, JCMsolve also has a number of built-in mesh adaption and/or local polynomial degree adaption schemes defined in the Refinement section. The refinement loop is intended to reach and check the Precision level, the user specified. The user can define a prerefinement of the mesh before the simulation is started. Further, a uniform or adaptive mesh refinement loop can be defined.