Stress¶
| Type: | 2-Tensor, or section |
|---|---|
| Range: | [v_1, …, v_9] |
| Default: | -/- |
| Appearance: | optional |
Specifies the mechanical stress 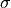 within the physical domain or boundary. The unit of the stress are pascals,
within the physical domain or boundary. The unit of the stress are pascals, 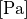 , which is equivalent newtons per square meter.
, which is equivalent newtons per square meter.
A constant stress can be defined by assigning a rank-2 tensor:
# define a constant stress
Stress = [..., ... , ...,
..., ... , ...,
..., ... , ...]
For more general cases, a stress field may be given as a section in order to deal with space, time, and parameter dependent definitions:
# define a force density as a section
Stress {
Constant {...}
Python {...}
...
}
Field definitions within this section are summed up. Consult the subsequent sections to see which types of field definitions are allowed.
Note
Within the context of linear continuum mechanics the stress is implicitly defined, when a displacement field 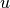 is defined.
is defined.
Then the stress is given by
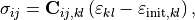
where 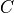 is the stiffness tensor,
is the stiffness tensor,  is the strain and
is the strain and  it the initial strain.
it the initial strain.