Expression¶
| Type: | string |
|---|---|
| Range: | [] |
| Default: | -/- |
| Appearance: | simple |
| Excludes: | Function, Module |
This parameter is used to define a tensor field of type “relative permittivity” by means of a Python expression within the .jcm input file. The syntax is the following:
RelPermittivity {
Python {
Expression = " ... # your python scripting
...
value = ... # set return value
"
# define one or more parameters
Parameter {
Name = "Para1"
...
}
Parameter {
Name = "Para2"
...
}
}
}
The string value Expression has to be valid Python code and is interpreted in the following way:
- The NumPy-package is automatically imported when evaluating the expression.
- Any parameter as defined by a
Parametersection is available within the Python expression as an NumPy object named accordingly to the value of the parameter Name. - The position
 and the time
and the time  are available as NumPy objects name
are available as NumPy objects name Xandtrespectively. - For time-harmonic electromagnetic problems the angular frequency
 can be addressed by
can be addressed by EMOmega, (EMstands for electromagnetic). - The expression must define a NumPy object named
valuewhich contains the return value of appropriate shape (relative permittivity is a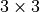 - matrix).
- matrix). - Keep in mind the Python indentation rule.
In a first practical example we want to give the  based definition of the relative permittivity, where
based definition of the relative permittivity, where  denotes the refractive index and
denotes the refractive index and  the extinction factor. We want to assume that the relative permittivity is
the extinction factor. We want to assume that the relative permittivity is  dependent in the following sense:
dependent in the following sense:

The corresponding .jcm snippet may look like this:
RelPermittivity {
Python {
Expression = "value = pow(nk[0]+1j*nk[1]/EMOmega), 2)*eye(3, 3)"
Parameter {
Name = "nk"
VectorValue = [..., ...] # set n,k here
}
}
}
As a second example we want to define a relative permittivity which varies with the temperature:
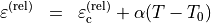
The first term is a constant value. The second term is a thermo-optical correction. This correction term has one field parameter - the temperature - and two coefficient parameters, the thermo-optical coefficient 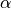 and a standard temperature value
and a standard temperature value 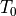 .
.
The overall relative permittivity definition may be defined as:
RelPermittivity {
Constant = ... # set first term eps_c, here
Python {
Expression = "value = a*eye(3, 3)*(T-T0)"
Parameter {
Name = "T"
FieldValue {
FieldBagPath = ... # path to a temperature field
Quantity = Temperature
}
}
Parameter {
Name = "a"
VectorValue = ... # scalar thermo-optical coefficient
}
Parameter {
Name = "T0"
VectorValue = ... # standard temperature
}
}
}