BayesLeastSquare¶
Purpose¶
The goal of the driver is to mininize the regression standard error as a function of the vector of model parameters 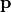 .
The regression standard error with respect to an observed target vector
.
The regression standard error with respect to an observed target vector
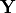 (e.g. a measurement) is defined as
(e.g. a measurement) is defined as
![\text{RSE}(\mathbf{p}) = \sqrt{[\mathbf{Y} - \mathbf{y}(\mathbf{p})]^T G^{-1} [\mathbf{Y} - \mathbf{y}(\mathbf{p})]/\text{DOF}},](_images/math/d866eac79b16544e814e259d7de136798560f5db.png)
where 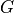 is the covariance matrix of the target vector entries and
is the covariance matrix of the target vector entries and
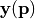 it the model vector, which depends on the
parameter values
it the model vector, which depends on the
parameter values 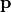 .
The number of degrees of freedom DOF is the difference between the length of the
target vector
.
The number of degrees of freedom DOF is the difference between the length of the
target vector 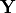 and the length of the parameter vector
and the length of the parameter vector
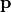 . If the number of degrees of freedom is negative, we set DOF=1.
The regression standard error is often also denoted as noise level or standard deviation STD. The square of the RSE is the the mean squared error MSE.
. If the number of degrees of freedom is negative, we set DOF=1.
The regression standard error is often also denoted as noise level or standard deviation STD. The square of the RSE is the the mean squared error MSE.
It is possible to retrieve the covariances between the model parameters at the found minimum of the RSE (see Driver-specific Information). The paramter covariance matrix  gives an estimate of the uncertainties of the reconstructed parameters under the assumption that the model vector entries
gives an estimate of the uncertainties of the reconstructed parameters under the assumption that the model vector entries 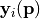 depend linearly on
depend linearly on 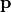 . The standard deviations of the parameter value
. The standard deviations of the parameter value  are given as
are given as 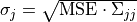 .
.
The driver performs a Gaussian process regression (GPR) on all entries of the
model vector 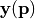 . From the regression model it determines
parameter values
. From the regression model it determines
parameter values 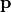 which lead to a large expected improvement of the regression standard error RSE. It converges typically faster than the standard least-square minimization, which is based on a Levenberg-Marquardt approach.
which lead to a large expected improvement of the regression standard error RSE. It converges typically faster than the standard least-square minimization, which is based on a Levenberg-Marquardt approach.
The GPR model contains higher order dependencies on 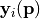 around the minimium of the RSE.
In order to determine the parameter uncertainties including non-linear terms, it is possible to sample the probability distribution of the reconstructed parameters using a Markov chain Monte Carlo sampling (study.run_mcmc()). For this sampling, it is also possible to define more complex error models (see error_model). After a MCMC sampling, the reconstructed parameter values are determined by the median value of the probability distribution. The lower uncertainty is given by the 16% quantile of the distribution and the upper uncertainty as the 84% quantile.
around the minimium of the RSE.
In order to determine the parameter uncertainties including non-linear terms, it is possible to sample the probability distribution of the reconstructed parameters using a Markov chain Monte Carlo sampling (study.run_mcmc()). For this sampling, it is also possible to define more complex error models (see error_model). After a MCMC sampling, the reconstructed parameter values are determined by the median value of the probability distribution. The lower uncertainty is given by the 16% quantile of the distribution and the upper uncertainty as the 84% quantile.
Usage Example¶
addpath(fullfile(getenv('JCMROOT'), 'ThirdPartySupport', 'Matlab'));
client = jcmwave_optimizer_client();
% Definition of the search domain
domain = {
struct('name','m', 'type','continuous', 'domain',[-5,5]),...
struct('name','b', 'type','continuous', 'domain',[0,10])...
};
% Creation of the study object with study_id 'example'
study = client.create_study('domain',domain, ...
'driver','BayesLeastSquare',...
'name','BayesLeastSquare example', ...
'study_id','BayesLeastSquare_example');
% Generate some randomized data for a linear fit
rand("seed", 1);
N = 50; %number of datapoints
X = sort(10 * rand(1,N)); %random x-values
m0 = -0.5; %slope
b0 = 5; %offset
f0 = 0.5; % Y-proportional error
Y = m0 * X + b0; %data points
% add error proportional to Y
Y = Y + f0 * abs(Y) .* (2*rand(1,N)-1);
% add error independent of Y with mean 0.1 and and std deviation 0.5
Yerr = 0.1 + 0.5 * rand(1,N);
Y = Y + Yerr .* (2*rand(1,N)-1);
% Definition of the objective function including derivatives
function obs = objective(sample)
pause(2.0); % makes objective expensive
m = sample.m;
b = sample.b;
obs = study.new_observation();
%objective
obs = obs.add(m*X+b);
%derivative w.r.t. m
obs = obs.add(X, 'm');
%derivative w.r.t. b
obs = obs.add(0*X+1, 'b');
end
% Set study parameters
study.set_parameters('target_vector',Y, 'uncertainty_vector', Yerr);
% Run the minimization
while(not(study.is_done))
sug = study.get_suggestion();
obs = objective(sug.sample);
study.add_observation(obs, sug.id);
end
% Least square error estimate
info = study.info();
driver_info = study.driver_info();
cov = driver_info.parameter_covariance;
MSE = driver_info.MSE; %mean squared error of residuum at minimum
err = sqrt(MSE*diag(cov)); %error estimate
fprintf('\nError estimates of least square minimization');
fprintf("\nm = %0.3f +/- %0.3f",info.min_params.m,err(1));
fprintf("\nb = %0.3f +/- %0.3f",info.min_params.b,err(2));
% The least square estimates are based on the uncertainty vector
% and the linear approximation of the model vector y(p).
% A Markov chain Monte Carlo (MCMC) sampling allows to determine
% the probability distribution of the model parameters including non-linear
% terms and a more realistic error model (see parameters section for details).
study.set_parameters(...
'error_model','sqrt(err_cov^2 + y_model^2 * exp(2*log_f))',...
'error_model_parameter_distribution',{...
struct('name','log_f','distribution','uniform','domain',[-10,1])...
}...
);
% The MCMC sampling with a more realistic error model gives more
% accurately reconstructed parameters.
mcmc_result = study.run_mcmc();
%MCMC sampling results: histograms and 16%,50%,84% quantiles
figure(2);
hist(mcmc_result.samples(:,1));
title_str = sprintf(['m: median %0.2f, lower uncertainty %0.2f ' ...
'upper uncertainty %0.2f'], mcmc_result.medians(1),...
mcmc_result.lower_uncertainties(1),mcmc_result.upper_uncertainties(1));
title(title_str);
figure(3);
hist(mcmc_result.samples(:,2));
title_str = sprintf(['m: median %0.2f lower uncertainty %0.2f ' ...
'upper uncertainty %0.2f'], mcmc_result.medians(2),...
mcmc_result.lower_uncertainties(2),mcmc_result.upper_uncertainties(2));
title(title_str);
Parameters¶
The following parameters can be set by calling, e.g.
study.set_parameters('example_parameter1',[1,2,3], 'example_parameter2',true);
| max_iter (int): | Maximum number of evaluations of the objective function (default: inf) |
|---|
| max_time (int): | Maximum run time in seconds (default: inf) |
|---|
| num_parallel (int): | |
|---|---|
| Number of parallel observations of the objective function (default: 1) | |
| distribution (list): | |
|---|---|
Definition of random distribution for each parameter in the format of a list. All continuous parameters with unspecified distribution are assumed to be uniformely distributed in the parameter domain. Fixed and discrete parameters are not random parameters. The value of discrete parameters defaults to the first listed value. (default: None)
|
|
| optimization_step_min (int): | |
|---|---|
| Minimum number of observations of the objective before the hyperparameters are optimized (default: 2 times number of dimensions). Note: Each derivative observation is counting as an independent observation (default: None) | |
| optimization_step_max (int): | |
|---|---|
| Maximum number of observations of the objective after which no more hyperparameter optimization is performed. Note: Each derivative observation is counting as an independent observation (default: 300) | |
| optimization_interval (int): | |
|---|---|
| Maximum number of observations of the objective after which the hyperparameters are optimized. Note: Each derivative observation is counting as an independent observation (default: 20) | |
| compute_suggestion_in_advance (bool): | |
|---|---|
| If True a suggestion is computed in advance to speed up the sample computation. (default: True) | |
| num_training_samples (int): | |
|---|---|
| Number of random initial samples before the samples are drawn according to the acquisition function. (default: 0) | |
| parameter_uncertainties (list): | |
|---|---|
Sometimes, one is interested in minima of the objective function that are preferably insensitive to variations of certain parameters (e.g. if the parameters have large fabrication variances). In this case, one can specify the uncertainties of those parameters, i.e. their standard deviations. The regression model of the objective is averaged over the uncertainty intervals such that very narrow local minima are averaged out whereas broad minima are not effected. Note that the averaging results in additional numerical effort that grows exponentially with the number of uncertain parameters. (default: None)
|
|
| optimization_level (float): | |
|---|---|
| Steers how often the hyper-parameters are optimized. Small values (e.g. 0.01) lead to more frequent optimizations. Large values (e.g. 1.0) to less frequent optimizations (default: 0.05) | |
| num_samples_hyperparameters (int): | |
|---|---|
| Number of local searches for optimal hyperparameters. If None, then the number is chosen accordingly to the number of dimensions. (default: None) | |
| num_fantasies (int): | |
|---|---|
| Number of “fantasy” samples drawn from the Gaussian process in order to average over uncertain function values. This is used for avoiding the position of running samples or to handle noisy inputs. (default: 18) | |
| matern_order (int): | |
|---|---|
| Order of the used Matern covariance function, i.e. for m=5 the Matern 5/2 function is used. (default: 5) | |
| length_scales (list): | |
|---|---|
| List of length scales for each parameter on which the objective functions varies. If not set, the length scales are chosen automatically. (default: None) | |
| detect_noise (bool): | |
|---|---|
| If true, variance due to noise is modelled by two hyperparameter (noise of objective and noise of derivatives). The value of the hyperparameters are chosen to maximize the likelihood of the observations. (default: False) | |
| noise_variance (list): | |
|---|---|
| List of noise variances for objective observations and derivative observations relative to total variance. If not set, noiseless observations are assumed. Note: If detect_noise is true, the noise variances will be optimized after optimization_step_min observations. (default: None) | |
| warp_input (bool): | |
|---|---|
| If true, the input function values are transformed (warped) in order to maximize the likelihood of the observations. (default: False) | |
| warping_strengths (list): | |
|---|---|
| List of lower and upper warping strength. If not set, function values are left unwarped. Note: If warp_input is true, the warping strengths will be optimized after optimization_step_min observations. (default: None) | |
| localize (bool): | |
|---|---|
| If true, a local search is performed, i.e. samples are not drawn in regions with large uncertainty. (default: False) | |
| horizon (int): | Horizon of previous observations to take into account for driver. (default: all previous observations are taken into account). (default: None) |
|---|
| max_scaling (float): | |
|---|---|
| Maximum scaling parameter. The scaling parameter is used to enforce a global search after convergence to a local minimum.It is automatically increased when a local convergence has been detected. (default: 10) | |
| eps (float): | Stopping criterium. Minimum distance in the parameter space to the currently known minimum (default: 0.0) |
|---|
| min_val (float): | |
|---|---|
| Stopping criterium. Minimum value of the objective function (default: -inf) | |
| strategy (str): | Sampling strategy of the Bayesian optimization. (default: EI) (options: [‘EI’, ‘LCB’, ‘PoI’]) |
|---|
| scaling (float): | |
|---|---|
| Scaling parameter of the model uncertainty. Default is scaling = 1.0 For scaling >> 1.0 (e.g. scaling=10) the search is more explorative. For scaling << 1.0 (e.g. scaling=0.1) the search becomes more greedy, i.e. any local minimum is intensively exploited (default: 1.0) | |
| vary_scaling (bool): | |
|---|---|
| If True the scaling parameter is randomly varied between 0.1 and 10 (default: True) | |
| post_converge (bool): | |
|---|---|
| Converge the minimization using probability of improvement after the min_PoI critereon has been met. (default: False) | |
| min_PoI (float): | |
|---|---|
| Stopping criterium. Minimum probability of improvement for the last 5 aqcuisitions (default: 0.0) | |
| min_EI (float): | Stopping criterium. Minimum expected improvement for the last 5 aqcuisitions (default: 0.0) |
|---|
| target_vector (list): | |
|---|---|
Vector of observations 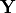 . (default: None) . (default: None) |
|
| covariance_matrix (matrix): | |
|---|---|
Covariance matrix 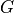 .
For a simple least-square minimization, .
For a simple least-square minimization, 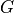 is the
identity matrix.
For measurements with different uncertainties is the
identity matrix.
For measurements with different uncertainties 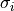 , ,
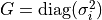 . If not specified, . If not specified, 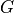 is the identity matrix. (default: None)
is the identity matrix. (default: None) |
|
| uncertainty_vector (list): | |
|---|---|
Defines the vector of measurement uncertainties
![\mathbf{s} = [\sigma_1,\sigma_2\dots]^T](_images/math/5f2f2ee0107f7fa195913a1ce88111690e4bc1f8.png) of the target vector
of the target vector 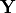 .
Accordingly, the covariance matrix is set to .
Accordingly, the covariance matrix is set to
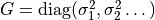 . (default: None) . (default: None) |
|
| error_model (string): | |
|---|---|
String defining error of measurement
|
|
| error_model_parameter_distribution (list): | |
|---|---|
Definition of random distribution for each parameter of the error model in the format of a list. For an example, see the documentation of error_model. (default: []) |
|
| post_converge_lm (bool): | |
|---|---|
| Converge the minimization using Levenberg-Marquardt minimization after the min_PoI critereon has been met. (default: True) | |
| explore_max_likelihood (bool): | |
|---|---|
If true, samples are drawn close to the maximum posterior likelihood where the uncertainty of the Gaussian process prediction is relatively large. Activating this option is useful prior to running a Makov chain Monte Carlo sampling of the posterior. (default: False)
|
|
| min_UC (float): | Stopping criterium used during “explore_max_likelihood”. Minimum average uncertainty of all Gaussian processes (in units of their global stamdard deviation) for the last 5 aqcuisitions (default: 0.001) |
|---|
| ftol (float): | Tolerance for termination by the change of the cost function while converging the results using Gauss-Newton minization. The optimization process is stopped when dF < ftol * F. (default: 1e-10) |
|---|
| max_data_hyper_optimization (int): | |
|---|---|
Maximum number of data points (objective and derivative observations for each input) for which a hyper parameter optimization is performed. The limit is only checked if the hyperparameters were at least optimized once. In None, the value is set to max(100*len(target_vector)*len(params),self.optimization_step_max). (default: None) |
|
| degrees_of_freedom (float): | |
|---|---|
| Number of degrees of freedeom (DOF) used for stochastic variable of the chi-squared distributio. This number indicates how many output channels of the forward model are statistically independent. Default: Automatically determined effective DOF. (default: None) | |
Driver-specific Information¶
A struct with following parameters can be retrieved by calling
study.driver_info().
| parameter_covariance: | |
|---|---|
Covariance matrix  of the parameters at the sampling point with minimal discrepancy. The uncertainty of the parameter of the parameters at the sampling point with minimal discrepancy. The uncertainty of the parameter 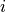 is given as is given as  . . |
|
| MSE: | The mean squared error MSE is the square of the regression standarderror (RSE). It is given as the residual sum of squares divided by the degrees of freedom (DOF), i.e. the length of the target vector M minus the number of parameters N: MSE=RSS/(M-N). |
|---|
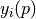 ) and the square root of the diagonal entry of the covariance matrix
) and the square root of the diagonal entry of the covariance matrix 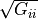 ). Other parameters with random distributions must be defined in the parameter “error_model_parameter_distribution”. The model error
). Other parameters with random distributions must be defined in the parameter “error_model_parameter_distribution”. The model error 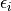 is used in the MCMC sampling to define the log likelihood as
is used in the MCMC sampling to define the log likelihood as ![ll = -0.5*\sum_i[(Y_i-y_i(p))^2/\epsilon_i^2 + \log(\epsilon_i^2)]](_images/math/80138fd156416977ddde6594746f4edf70750af7.png) .If not specified, the error model is
.If not specified, the error model is