Lattice Copies

Learning targets

• copy a geometrical primitive to lattice positions

Many geometries like photonic crystals are constructed by a replication of a unit cell geometry at the certain positions of a lattice. This can easily done within JCMgeo as shown by the following example:

.jcm Input File

• layout.jcm [ASCII]

   Layout2D {  
     Name = "PhC-Waveguide"  
     UnitOfLength = 1e-09  
     Objects {
       Parallelogram {
         Priority = ComputationalDomain
         DomainId = 1
         BoundingBox {
           Offset = [50 50 50 50]
         }
       }
       
       Circle {   
         DomainId = 2 
         RefineAll = 2 
         Radius = 200 
         LatticeCopies { 
           LatticeVectorLengths = [500 500] 
           LatticeAngle = 90
           Positions { 
             IndexShiftY = 0
             RangeStart = [0 0]
             DomainIds = [0 0 0 0 2 0 2 0 0 0 0;
                          0 0 0 2 2 0 2 2 0 0 0;
                          0 0 2 2 2 0 2 2 2 0 0;
                          0 2 2 2 2 0 2 2 2 2 0;
                          2 2 2 2 2 0 2 2 2 2 2]
            } 
         } 
       }  
     }  
   }
   
  

This example is based on a square lattice. Changing the LatticeCopies section to

LatticeCopies {
  LatticeVectorLengths = [500 500]
  LatticeAngle = 60
  LatticeRotation = 90
  Positions {
    IndexShiftY = -1
    RangeStart = [0 -10]
    DomainIds = [2 0 0 0 0;
                 2 0 0 0 0;
                 2 2 0 0 0;
                 2 2 0 0 0;
                 2 2 2 0 0;
                 2 2 2 0 0;
                 2 2 2 2 0;
                 2 2 2 2 0;
                 4 2 2 2 2;
                 2 2 2 2 2;
                 0 0 0 0 0;
                 2 2 2 2 2;
                 5 2 2 2 2;
                 2 2 2 2 0;
                 2 2 2 2 0;
                 2 2 2 0 0;
                 2 2 2 0 0;
                 2 2 0 0 0;
                 2 2 0 0 0;
                 2 0 0 0 0;
                 2 0 0 0 0]
  }
}

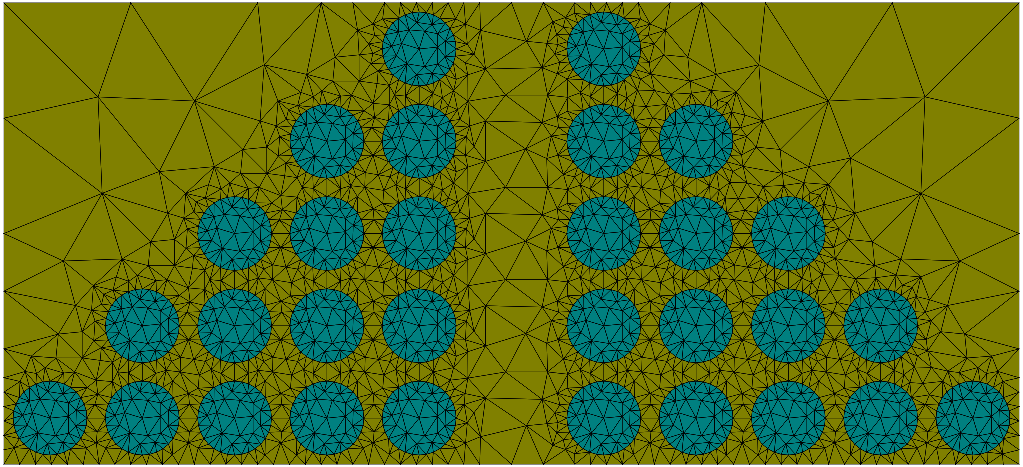
gives the following waveguide-like structure with a underlying hexagonal lattice: