Z-Corner Rounding¶
Learning targets
- Use scripting to describe a complicated dependency in
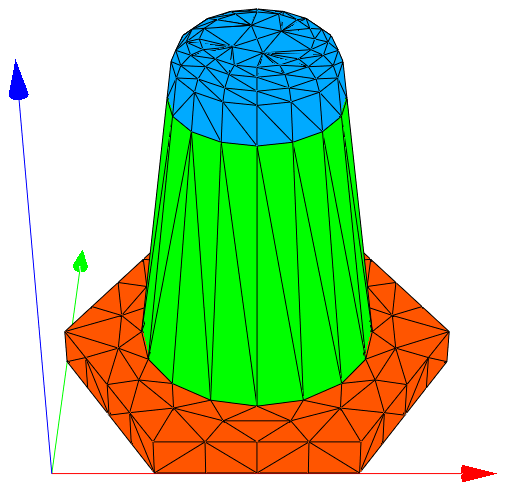
This example describes a unit cell of a hexagonal lattice
(equilateral triangular lattice) of cones with capping layer
and corner rounding.
The computational domain is specified as extruded polygon,
the cone is specified as extruded circle where radius and material
change with the z-coordinate.
The x- and y-positions of the polygon
points as well as the height-dependence of the cone parameters
are computed in few lines of Matlab code in a template file
which is run from a script (please see also the
documentation for the JCMsuite
Matlab?? Interface).
The following figure shows an image of parts of the geometry and mesh:
Input Files
layout.jcm [ASCII]
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85
Layout3D { Name = "TutorialExample3D" UnitOfLength = 1e-09 MeshOptions { MaximumSideLength = 100 MinimumMeshAngle = 20 } Extrusion { Objects { Polygon { Name = "ComputationalDomain/Air" DomainId = 101 Priority = -1 Points = [125.000 216.506 -125.000 216.506 -250.000 0.000 -125.000 -216.506 125.000 -216.506 250.000 -0.000] Boundary { Number = [1 2 3 4 5 6] Class = Periodic } } Circle { DomainId = 102 Radius = 123.601319405876 RefineAll = 1 } } MultiLayer { LayerInterface { GeometryValues = [Circle{1}/Radius:156.139] BoundaryClass = Transparent } Layer { Thickness = 50 DomainIdMapping = [101 1, 102 1] } LayerInterface { GeometryValues = [Circle{1}/Radius:150.000] } Layer { Thickness = 350 DomainIdMapping = [101 4, 102 2] } LayerInterface { GeometryValues = [Circle{1}/Radius:107.025] } Layer { Thickness = 50 DomainIdMapping = [101 4, 102 3] } LayerInterface { GeometryValues = [Circle{1}/Radius:100.886] } Layer { Thickness = 15 DomainIdMapping = [101 4, 102 3] } LayerInterface { GeometryValues = [Circle{1}/Radius:95.025] } Layer { Thickness = 10.9807621135332 DomainIdMapping = [101 4, 102 3] } LayerInterface { GeometryValues = [Circle{1}/Radius:82.696] } Layer { Thickness = 4.01923788646684 DomainIdMapping = [101 4, 102 3] } LayerInterface { GeometryValues = [Circle{1}/Radius:67.203] } Layer { Thickness = 50 DomainIdMapping = [101 4, 102 4] } LayerInterface { GeometryValues = [Circle{1}/Radius:91.063] BoundaryClass = Transparent } } } }Matlab script run_geometry.m [ASCII]
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
% Interface for 3D unit cell of a hexagonal lattice % 2D-periodic hexagonal array of 3D cones % with capping layer and with corner rounding keys.uol = 1e-9; keys.p = 500.0; % periodicity length keys.h1 = 350.0; % height of lower material keys.h2 = 80.0; % height of top material (capping layer) keys.radius_bottom = 150; % cone radius bottom keys.cone_swa = 83.0; % cone sidewall angle keys.corner_rounding_r = 30.0; % top corner rounding radius keys.corner_rounding_n = 2; % corner rounding number of segments keys.slc1 = 100; % maximum triangle sidelength jcmwave_geo('.', keys, 'jcmt_pattern', 'matlab', 'show', inf);Layout template file layout.matlab.jcmt [ASCII]
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95
<? % Matlab definition of a hexagon angles = [1:6]*2*pi/6; points = keys.p/2*exp(1i*angles); keys.points_cd(1:2:12) = real(points(:)); keys.points_cd(2:2:12) = imag(points(:)); % build the cone from layers of different heights offset = 50; % computational domain offset in +/-z-direction heights = [-offset, 0, keys.h1, keys.h1 + keys.h2, keys.h1 + keys.h2 + offset]; % additional corner rounding at the top angles = linspace(0, 90, keys.corner_rounding_n + 2); r = keys.corner_rounding_r; heights = unique([heights keys.h1 + keys.h2 - r + r*sind(angles)]); % thicknesses of the different layers thicknesses = heights(2:end) - heights(1:end-1); % radii of the cone at different heights radii = keys.radius_bottom - tand(90-keys.cone_swa)*heights; keys.radius_mean = radii(1)/2+radii(end)/2; indices_rounded_corner = find(heights >= keys.h1 + keys.h2 - r ... & heights <= keys.h1 + keys.h2); radii(indices_rounded_corner) = radii(indices_rounded_corner) - r*(1 - cosd(angles)); ?> Layout3D { Name = "TutorialExample3D" UnitOfLength = %(uol)e MeshOptions { MaximumSideLength = %(slc1)e MinimumMeshAngle = 20 } Extrusion{ Objects { Polygon { Name = "ComputationalDomain/Air" DomainId = 101 Priority = -1 Points = %(points_cd)3f <? for counter = 1:length(keys.points_cd)/2 keys.number_ = counter; ?> Boundary { Number = %(number_)i Class = Periodic } <? end ?> } Circle { DomainId = 102 Radius = %(radius_mean)e RefineAll = 1 } } MultiLayer { <? for counter = 1:length(thicknesses) keys.thickness_ = thicknesses(counter); keys.radius_ = radii(counter); if heights(counter) < 0 keys.material_1 = 1; keys.material_2 = 1; elseif heights(counter) < keys.h1; keys.material_1 = 4; keys.material_2 = 2; elseif heights(counter) < keys.h1+keys.h2; keys.material_1 = 4; keys.material_2 = 3; else keys.material_1 = 4; keys.material_2 = 4; end ?> LayerInterface { GeometryValues = [Circle{1}/Radius:%(radius_)3f] <? if counter==1 ?> BoundaryClass = Transparent <? end ?> } Layer { Thickness = %(thickness_)e DomainIdMapping = [101 %(material_1)i, 102 %(material_2)i] } <? end keys.radius_ = radii(counter+1); ?> LayerInterface { GeometryValues = [Circle{1}/Radius:%(radius_)3f] BoundaryClass = Transparent } } } }