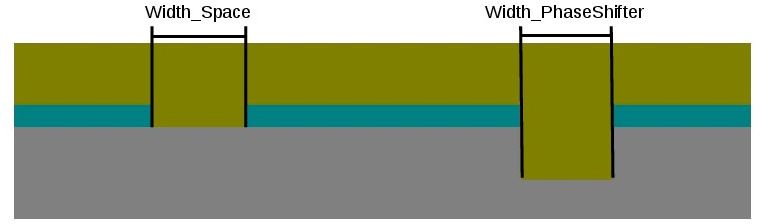Reduced Basis Method

Introduction

A number of optical applications require simulation of a basic system setup in a large number of different configurations. Examples are scatterometry, where a number of geometrical or material parameters are varied and reconstructed from optical measurements, source mask optimization in lithography, or general optimizations of nano optical systems such as light sources, out-coupling structures, or solar cells.

Such systems have a given setup, which is described by a finite number of variable parameters which are allowed to vary in a given range.

Performing a large number of simulations for fixed parameter set values are often numerically very costly and even prohibit a number of applications. E.g. in scatterometry large libraries are precomputed to enable real-time reconstruction of parameters in a measurement. But even construction of such libraries itself can be prohibitively expensive from a practical point of view.

Basic idea

The reduced basis method is a very efficient technique to simulate parametrized systems for a large number of realizations [Pomplun]. The basic idea is a online-offline decomposition of the parametrized systems. In the offline phase, the parametrized system is simulated for a number of different configurations. In the online phase these solutions are used to obtain results for arbitrary parameters within specified parameter intervals. The more solutions, so called “snapshots” are computed in the offline phase and included into the reduced basis representation of the system, the more accurate the results of the online phase are. Usually the reduced basis method converges much faster than interpolation techniques, because of a number of reasons. First, the parameter realizations chosen in the offline phase are based on error estimation techniques, which guarantee that a maximum of new information about the parametrized system is included into the basis. Second, in the offline phase all snapshots computed in the offline phase contribute to the solution. In interpolatory methods, often e.g. only nearest neighbours are used to construct an unknown solution of the parameter space.

The Attenuated Phase Shift Mask tutorial is used as an example to explain setup and usage of the reduced basis method.

Example setup

The variable parameters for construction of the reduced model for this example are chosen as the widths of the line openings of the phase shift mask. In order to define a parameter as variable, the syntax used to define parameter derivatives is used:

DerivativeParameter {
  Name = "Width_Space"
  TreeEntry = Layout2D/Objects/Parallelogram{1}/Width
}

DerivativeParameter {
  Name = "Width_PhaseShifter"
  TreeEntry = Layout2D/Objects/Parallelogram{2}/Width
}


Layout2D {
  Name = "AttPSM"
  UnitOfLength = 1e-06
  MeshOptions {
    MaximumSideLength = 0.05
  }
  Objects {    
    MultiLayer {
      Name = "MaskLayers"
      Width = 2.4
      Layer {
        DomainId = 3
        Height = 0.3
      }
      Layer {
        DomainId = 2
        Height = 0.072
      }
      Layer {
        DomainId = 1
        Height = 0.2
      }
      Port = North
      GlobalPosition = [0 0.2]
      
      Boundary {
        Number = [North, South]
        Class = Transparent
      }
      Boundary {
        Number = [East, West]
        Class = Periodic
      }      
    }
    
    Parallelogram {
      Name = "Space"
      Height = 0.072
      Width = 0.4
      DomainId = 1
      Port = North
      GlobalPosition = [-0.6 0]
    }
    
    Parallelogram {
      Name = "PhaseShifter"
      Height = 0.244
      Width = 0.4
      DomainId = 1
      Port = North
      GlobalPosition = [0.6 0]
    }
  } 
}

Both widths of the parallelograms are introduced as DerivativeParameter and named Width_Space and Width_PhaseShifter:

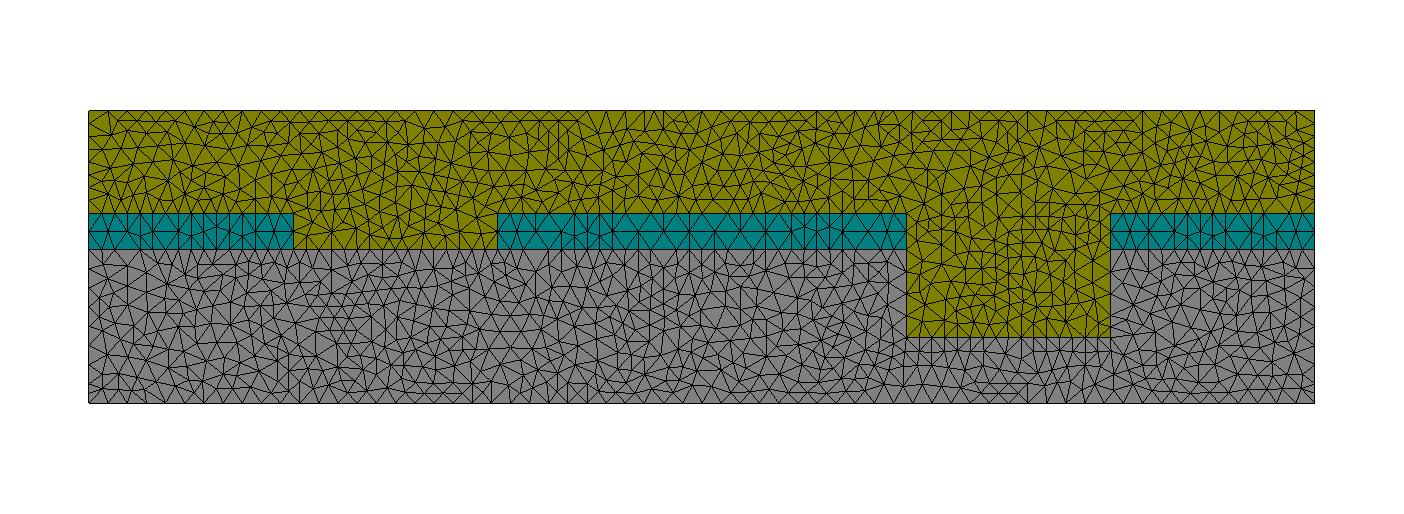
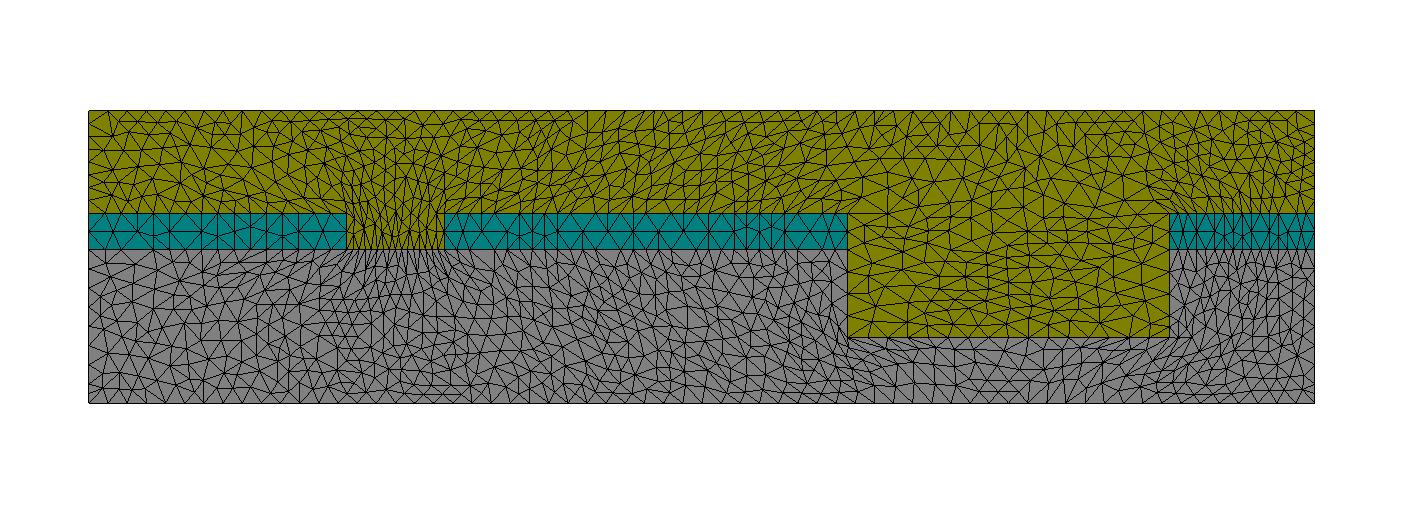
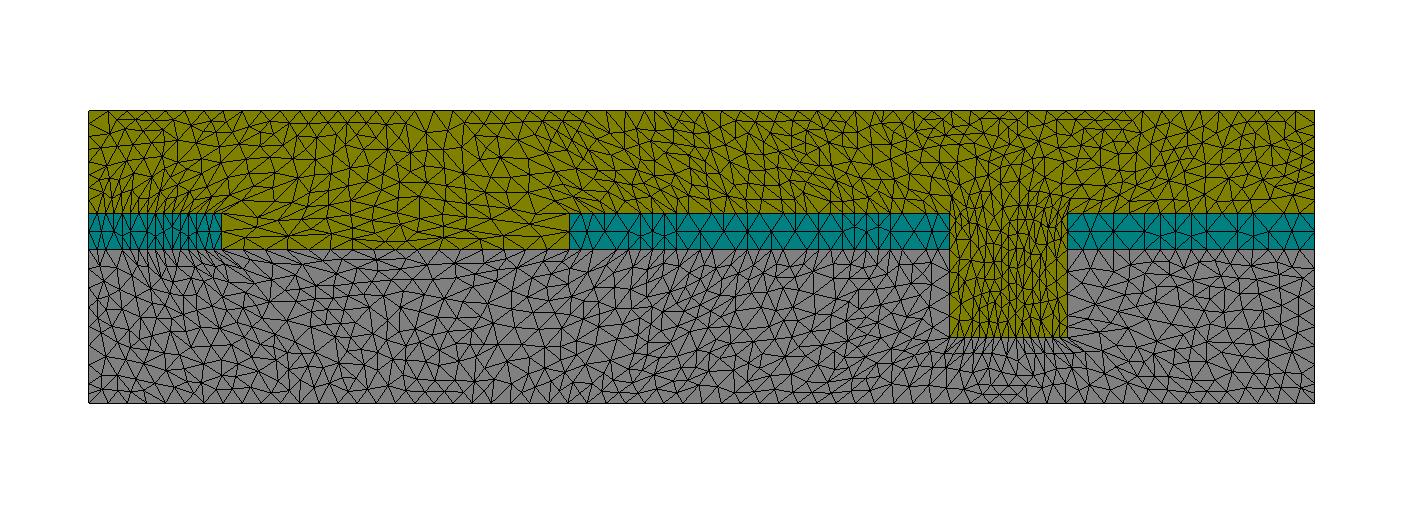
The resulting mesh, created by JCMgeo, is parametrized by these user defined parameters, and can be visualized with JCMview. Below, a number of parameter configurations are shown, together with their displaced meshes:

Besides introduction of parameters in layout.jcm file, the remaining project files are exactly as in the original tutorial example.

Reduced Basis setup

The creation of the reduced basis model is controlled in the file create_rb.jcmp:

PostProcess {
  CreateReducedBasis {
    ProjectFileName = "./project.jcmp"
    OutputFileName = "./rb.jcm"

    TargetPostProcessAccuracy = 1e-3
    NTrainingSolvesMax = 50
    IntermediateResultBackup = 5

    ProjectParameters {
      Grid {
        Parameter{
          Name="Width_Space"
          Value=[-0.15,0.15]
        }
        Parameter{
          Name="Width_PhaseShifter"
          Value=[-0.15,0.15]
        }
      }
    }
  }
}

In the ProjectParameters section the parameter ranges for the reduced basis model are defined. Here, the chosen geometrical parameters are defined together with their ranges. Note, that the values are given as an offset with respect to the nominal width values of 0.3 specified for the parallelograms of the layout. Hence Width_Space = 0.1 gives a mask with line width Width = 0.3 + 0.1 = 0.4.

The self-adaptive construction process will generate a reduced model which gives valid results within the specified parameter ranges. Increasing ranges or number of parameters will normally lead to longer construction times. The final accuracy of the reduced model within the parameter ranges is defined by TargetPostProcessAccuracy and the construction is stopped, when the accuracy level is reached. Further, a maximum number of snapshot solutions NTrainingSolvesMax = 50 is given, as an upper limit of the dimension of the created reduced basis. Note that currently, reduced basis models can only be assembled for FourierTransform post processes.

During the construction of the reduced model, the simulation project defined by ProjectFileName is solved several times for different parameter configurations. The project file has to reside within a valid simulation folder including all necessary JCM files. The file name for the constructed reduced model is defined by OutputFileName.

As an optional parameter IntermediateResultBackup = 5 is set. This leads to an intermediate backup of reduced basis approximations of dimensions 5, 10, 15, 20, … Since the construction of the reduced model can be time-consuming it can be helpful to analyze already constructed reduced models, without interrupting the construction process itself.

Reduced Basis assembling

When the reduced basis construction process is started via:

>> JCMsolve --solve create_rb.jcmp

simulation flow is as follows. First, a reference project is solved to setup finite element degrees, transparent boundary conditions etc. Next a parameter dependent decomposition of the right hand side and finite element matrix are generated. Finally, the reduced basis model is built by successively adding snapshot solutions for different parameters. These parameters are chosen self-adaptively by a greedy strategy with output as follows:

              Reduced Model Convergence
dimension  max estimated error  Width_Space  Width_PhaseShifter
     1                  inf            0                   0
     2            1.678e-01        0.075               0.075
     3            1.266e-01       -0.075               0.075
     4            6.931e-02        0.075              -0.075
     5            2.353e-02       0.1125             -0.1125
     6            2.183e-02      -0.1125              0.1125
     7            1.553e-02       0.1125              0.1125
     8            2.297e-02       -0.075              -0.075
     9            1.032e-02      -0.1125              0.0375
    10            7.312e-03       0.0375             -0.1125
    11            2.951e-03      -0.1125             -0.1125
    12            2.681e-03     -0.09375             0.13125
    13            2.432e-03       0.1125              0.0375
    14            1.760e-03      -0.1125             -0.0375
    15            1.286e-03     -0.13125            -0.13125
    16            1.103e-03     -0.09375            -0.13125
    17            8.201e-04      0.13125            -0.09375
    18            6.462e-04       0.0375              0.1125
    19            4.724e-04      0.13125            -0.13125
    20            4.371e-04     -0.13125             0.13125
    21            2.550e-04       0.1125             -0.0375
    22            2.340e-04      -0.0375              0.1125

This table shows the convergence of the reduced basis model in dependence on its dimension, i.e. number of included snapshots. The parameters of the snapshots are reported, together with the maximum estimated error of the model over the user defined parameter range. We observe exponential convergence of the reduced basis approximation which is superior to interpolatory methods.

Reduced Basis evaluation

Once the reduced basis model is created, it can be evaluated extremely fast. Now arbitrary parameter values within the previously defined user intervals can be specified an the model is solved for these parameters. First, we choose parameters Width_Space = 0.1 and Width_PhaseShifter = 0.1 which correspond to the Attenuated Phase Shift Mask tutorial setup:

>> JCMsolve --solve solve_rb.jcmp

This online solution of the reduced model is configured in solve_rb.jcmp file:

PostProcess {
  EvaluateReducedBasis {
    ReducedBasisFileName = "./rb.jcm"
    ProjectFileName = "./project.jcmp"
    OutputFileName = "./rbSol.jcm"

    Format = JCM-ASCII

    EstimateError = yes
    ProjectParameterMappingFileName = "./paraMapping.jcm"

    ProjectParameters {
      Grid {
        Parameter{
          Name="Width_Space"
          Value=[0.1]
        }
        Parameter{
          Name="Width_PhaseShifter"
          Value=[0.1]
        }
      }
    }
  }
}

First, the reduced basis model, and the original project files are specified by ReducedBasisFileName and ProjectFileName. The reduced basis coefficients stored in OutputFileName, give the weights of the snapshots of the model which were taken in the offline phase. If EstimateError = yes is set, also an estimate of the solution quality for this parameter is given. In the ProjectParameters section, the parameters are specified, for which the reduced model is solved. The reduced basis solution for the Fourier coefficients is stored in the project_results\ft_rb_Para1.jcm file. A comparison to the Fourier coefficients of the Attenuated Phase Shift Mask tutorial show nice agreement.

Finally, the reduced model can be evaluated on the entire parameter region:

In the solve_rb_scan.jcmp file :

PostProcess {
  EvaluateReducedBasis {
    ReducedBasisFileName = "./rb.jcm"
    ProjectFileName = "./project.jcmp"
    OutputFileName = "./rbSol.jcm"

    Format = JCM-ASCII

    EstimateError = yes
    ProjectParameterMappingFileName = "./paraMapping.jcm"

    ProjectParameters {
      Grid {
        Parameter{
          Name="Width_Space"
          Value=[-0.1 : 0.01 : 0.1]
        }
        Parameter{
          Name="Width_PhaseShifter"
          Value=[-0.1 : 0.01 : 0.1]
        }
      }
    }
  }
}

Here, a Cartesian mesh in parameter space is defined, where the reduced model is evaluated. More than 400 solutions are computed in a few seconds!

The file specified by ProjectParameterMappingFileName includes the mapping of parameter values of the online scan to the file indices of project_results\ft_rb_Para*.jcm.

Bibliography

[Pomplun]

Pomplun, Reduced basis method for electromagnetic scattering problems, dissertation (2010). [http://www.diss.fu-berlin.de/diss/receive/FUDISS_thesis_000000017571]